در این آموزش از سری آموزشهای گام به گام نرم افزار Hspice ابتدا نیم نگاهی مختصر به جمع کننده ها خواهیم داشت و در مورد کاربرد آنها در مدارات دیجیتال و انواع مختلف جمع کننده ها از منظر فاکتور سرعت ، توان که یک اصل اساسی در طراحی مدارات دیجیتال است و همیشه باید بین این دو مصاحه برقرار کرد ، خواهیم پرداخت.
و در بخش بعدی طراحی مدارات داخلی یک جمع کننده سربار نردبانی یا جمع کننده رقم نقلی موجی (Ripple Carry Adder) که به اختصار RCA هم خوانده می شود را مورد بررسی قرار می دهیم و در انتها شبیه سازی جمع کننده رقم نقلی موجی چهار بیتی را در نرم افزار Hspice انجام خواهیم داد.
جمع کننده ها در یک نگاه
یک جمع کننده عمل جمع دودویی اعداد باینری را انجام می دهد. از جمع کننده ها علاوه بر جمع اعداد باینری برای کاربردهای زیاد دیگری از جمله تفریق کننده ، ضرب کننده ، مقایسه گر دودویی ، اکومولاتور و … نیز استفاده می شود که اهمیت آنها در مدارات دیجیتال را نشان می دهد. که سلولهای تشکیل دهنده جمع کننده ها شامل تمام جمع کننده (Full Adder) و نیم جمع کننده (Half Adder) می باشد. شکل زیر جدول صحت و شماتیک مداری یک نیم جمع کننده را نشان می دهد.
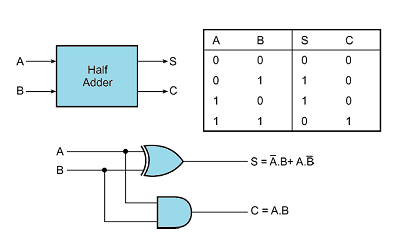
همانطور که می بینیم یک نیم جمع کننده شامل دو ورودی باینری A , B و دو خروجی جمع (s مخفف sum) و رقم نقلی (c مخفف carry) است و مطابق جدول هر گاه یکی از ورودی ها صفر و دیگری یک باشد خروجی s=1 و c=0 خواهد بود و اگر ورودی ها همزمان صفر باشند هر دو خروجی برابر صفر بوده و در تنها در صورتی که هر دو ورودی یک باشد خروجی c=1 خواهد بود. و بر طبق جدول می توان تابع S را با یک گیت XOR و تابع C را با یک گیت AND پیاده سازی کرد.
یک تمام جمع کننده علاوه بر جمع دو عدد باینری ، عمل جمع رقم نقلی حاصل از طبقات قبلی را نیز انجام می دهد. جدول درستی یک تمام جمع کننده را در شکل زیر مشاهده می کنیم. که ورودی های A,B اعداد باینری ورودی ، Cin رقم نقلی ورودی که از طبقات قبلی می آیند ، s خروجی جمع و Cout رقم نقلی خروجی است.
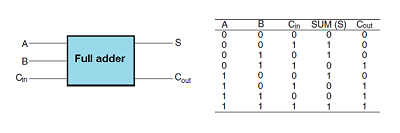
اگر جدول صحت مربوط به تمام جمع کننده را وارد جدول کارنو کنیم و ساده سازی را انجام دهیم توابع s و cout به صورت زیر ساده سازی خواهند شد.
S=A ⨁B ⨁C
Cout=AB+BCin+CinA
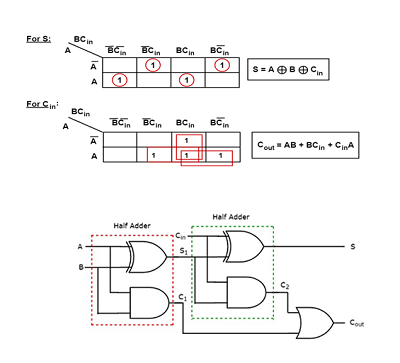
با کمی دقت در توابع خروجی در خواهیم یافت که می توان یک تمام جمع کننده را از دو نیم جمع کننده و یک گیت OR ساخت به این صورت که با چینش آنها توابع خروجی s , cout قابل حصول خواهند شد که تحلیل آن را به خواننده واگذار می کنیم.
جمع کننده ها بر اساس آرایشهای متفاوتی که به خود می گیرند انواع مختلفی دارند که همیشه بین پارامترهای سرعت ، توان مصرفی و فضای اشغالی توسط جمع کننده ها تناقض وجود دارد مثلاً یک جمع کننده سربار نردبانی ساده ترین نوع جمع کننده است که کمترین فضای ممکن را اشغال می کند و مصرف توان آن نیز نسبت به بقیه کمتر است اما نسبت به سایر جمع کننده ها کند است به خصوص اگر تعداد بیتهای آن افزایش یابد.
اما یک جمع کننده درختی (tree adder) در مقایسه با جمع کننده سربار نردبانی سرعت بالایی را در ازای افزایش پیچیدگی و توان مصرفی بیشتر نتیجه می دهد. بنابراین همیشه باید در مدارات دیجیتال مساله مصالحه (trade off) را در نظر داشت به این معنی که بهبود یک پارامتر نباید باعث شود بقیه پارامترها به کلی نادیده گرفته شوند.
علاوه بر پارامترهای سرعت و توان پارامترهای دیگری نیز از جمله فضای اشغالی ، گلیچ ، منظم بودن Layout و مسایل دیگر نیز در طراحی مدارات دیجیتال دخیل هستند اما این دو از اهمیت ویژه ای بر خوردار می باشند.
جمع کننده سربار نردبانی (RCA)
یک جمع کننده سربار نردبانی که به آن جمع کننده رقم نقلی موجی هم می گویند از پشت سر هم قرار گرفتن تمام جمع کننده ها تشکیل می شود.
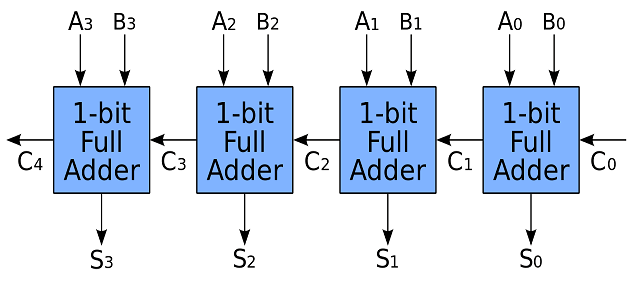
شیوه کار جمع کننده رقم نقلی موجی بسیار ساده بوده و بدین صورت است که هر طبقه دو رقم ورودی و رقم نقلی تولیدی حاصل از طبقات قبلی را جمع می کند و دو خروجی sum و carry تولید خواهد کرد ، خروجی s به عنوان خروجی هر طبقه به طور مستقیم مورد استفاده قرار می گیرد و خروجی c با بیت های طبقه بعدی جمع خواهد شد.
این روند تا انتها ادامه می یابد و بیت های رقم نقلی به صورت موجی از یک طبقه به طبقه بعدی خواهند رفت (دلیل نام گذاری جمع کننده رقم نقلی موجی همین است) تا در انتها یک رقم نقلی خروجی (در این مثال چهار بیتی C4) تولید شود که به عنوان با ارزش ترین بیت خروجی در جمع کننده مورد استفاده قرار خواهد گرفت.
پس در یک جمع کننده رقم نقلی موجی هر طبقه باید منتظر بماند تا طبقه قبلی رقم نقلی را تولید کند ، و اگر تعداد بیت های این جمع کننده افزایش یابد تاخیر قابل ملاحظه ای خواهیم داشت ، بنابراین برای تعداد بیت های بالا از سایر جمع کننده ها با توجه به مشخصات مورد نیاز برای طراحی استفاده خواهیم کرد.
نکته۱: در یک جمع کننده سربار نردبانی رقم نقلی ورودی اولین طبقه (C0) را صفر در نظر می گیریم و آن را به زمین وصل خواهیم کرد.
نکته۲: اگر جمع کننده سربار نردبانی چهار بیتی را به صورت یک جعبه در نظر بگیریم که تعدادی ورودی و خروجی داشته باشد ، ورودی ها شامل C0 و A0-A3 و B0-B3 خواهند بود و خروجی ها شامل S0-S3 وC4 بوده که به ترتیب C4 ، S3 ، S2 ، S1 ، S0 بیت های با ارزش خروجی هستند.
نکته۳: بیت های C1,C2,C3 در جمع کننده رقم نقلی موجی به عنوان نودهای داخلی مورد استفاده قرار می گیرند و در ارزش گذاری بیت های خروجی بی تاثیر هستند.
نکته۴: جمع دو عدد n بیتی n+1 بیت در خروجی تولید خواهد کرد.
طراحی مدارات داخلی جمع کننده سربار نردبانی
همانطور که در بخش قبلی دیدیم یک جمع کننده سربار نردبانی n بیتی از n عدد تمام جمع کننده تشکیل یافته و تمام جمع کننده از گیت های AND , OR , XOR ساخته می شود. پس کاری که باید انجام دهیم طراحی مدارات داخلی گیت های منطقی گفته شده در لاجیک مورد نظرمان است. لاجیک انتخابی ما برای طراحی گیت های منطقی لاجیک استاتیک می باشد.
دلیل انتخاب این لاجیک توان مصرفی پایین آن است که به دلیل نداشتن جریان ایستایی که از منبع تغدیه به سمت زمین جاری هست به لحاظ توان مصرفی نسبت به سایر لاجیک ها برتری دارد به علاوه نیاز به clk هم ندارد که این به ساده تر شدن طراحی مدارات کمک می کند.
شکل زیر منطق استاتیک را برای طراحی گیت های منطقی نشان می دهد.
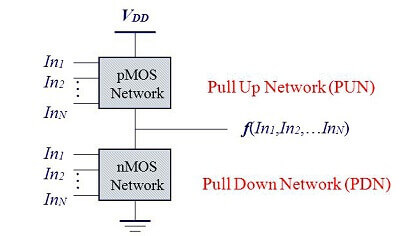
همانطور که می بینیم این لاجیک از دو شبکه بالاکش (Pull Up Network) و پایین کش (Pull Down Network) که به اختصار PUN , PDN خوانده می شوند تشکیل یافته که شبکه PUN شامل ترانزیستورهای PMOS و شبکه PDN شامل ترانزیستورهای NMOS می باشد و نحوه پیاده سازی اینها به گونه است که شبکه بالاکش مکمل شبکه پایین کش می باشد.
پس هیچگاه به طور همزمان شبکه PUN و PDN روشن نمی شوند بنابراین جریان ثابتی (جریان ایستا) که از سمت VDD به زمین جاری باشد وجود ندارد و این مهمترین مزیت کار با این لاجیک است.
برای کسب اطلاعات بیشتر در مورد لاجیک استاتیک و سایر لاجیک های دیگر به فصل ششم کتاب RABAEY (طراحی دریچه های منطقی ترکیبی) رجوع کنید.
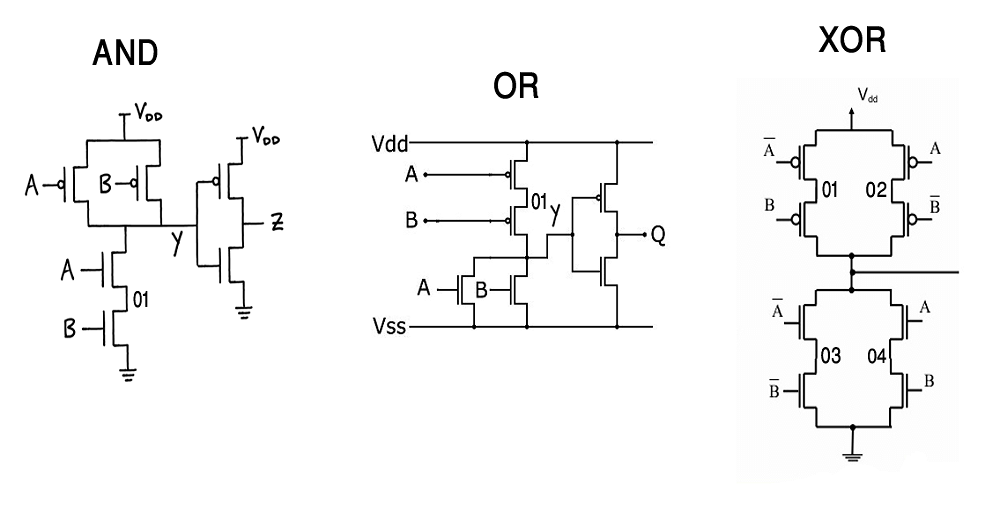
گیت های AND, OR, XOR در لاجیک استاتیک به صورت زیر پیاده سازی می شوند.
برای تمرین کار با زیر مدارات هر کدام از این گیت ها را به صورت یک زیر مدار جداگانه در نظر گرفته و نهایتاً تمام جمع کننده را که هسته اصلی جمع کننده سربار نردبانی است را هم به صورت یک زیر مدار که از زیر مدارهای سطح پایین تر (گیت های منطقی) تشکیل شده در خواهیم آورد و نت لیست مان را می نویسیم.
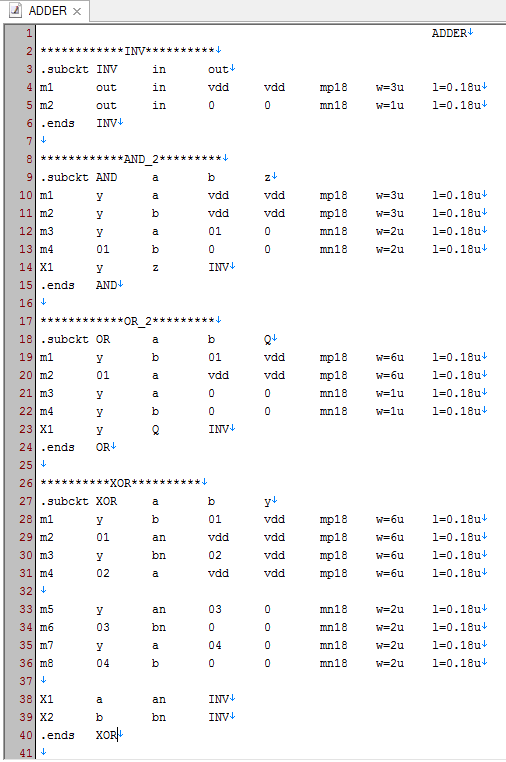
نت لیست گیت های منطقی را که به صورت زیر مدار در آورده ایم به شکل زیر می نویسیم.
نحوه سایز بندی ترانزیستورها در مدارات دیجیتال بدین صورت است که ترانزیستورهایی که به صورت سری پشت سر هم قرار می گیرند سایزشان را n برابر کرده (n تعداد ترانزیستورهای سری شده است) و سایز ترانزیستورهایی را که در مسیر موازی قرار دارند را تغییر نمی دهیم.
به طور مثال درگیت AND دو ورودی که دو ترانزیستور nmos پشت سر هم قرار می گیرند ، سایز nmos را که در حالت معمول برابر ۱um در نظر می گرفتیم دو برابر کرده و سایز ترانزیستور pmos را که معمولاً سه برابر nmos در نظر می گیرند تغییر نمی دهیم ،در گیت OR سایز nmos را بدون تغییر باقی می گذاریم و سایز pmos را دو برابر می کنیم و در گیت XOR چون هم nmos ها و هم pmos ها با هم سری هستند سایز هر دو را دو برابر می کنیم.
در تعریف گیت XOR به صورت زیر مدار از یک زیر مدار سطح پایین تر (گیت not) برای معکوس کردن ورودی های A , B که در شماتیک آن به صورت `A` , B نشان دادیم استفاده کرده و در نت لیست با نام an و bn تعریف نموده ایم. و در گیت های AND , OR هم همین کار را انجام خواهیم داد یعنی به فرض مثال یک گیت NOR را اگر not کنیم گیت OR حاصل می شود.
نکته۵: مبنای سایز بندی در مدارات دیجیتال را بر اساس گیت not می سنجیم به طور مثال اگر سایز ترانزیستورهای nmos و pmos در اینورتر به ترتیب برابر ۱um و ۳um باشد این سایز بندی را برای گیت های دیگر نیز در نظر خواهیم داشت ولی اگر نسبت ها را بخواهیم عوض کنیم مثلاً نسبت pmos به nmos را دو برابر انتخاب کنیم این مساله را باید در بقیه مدارات هم در نظر گرفت.
نکته۶: نودهای ۰۱ و ۰۲ و ۰۳ و ۰۴ به عنوان نودهای داخلی تعریف شده و می توانیم آنها را برای تمامی زیر مدارات تکرار کنیم.
حال که گیت های منطقی را به صورت زیر مدار تعریف کردیم می توانیم از آنها در هر جایی از نت لیست مان استفاده کنیم. اکنون نوبت به تعریف تمام جمع کننده که هسته اصلی جمع کننده سربار نردبانی است می رسد و همانطور که قبلاً هم اشاره نمودیم تمام جمع کننده را از زیر مدارهای سطح پایین تر خواهیم ساخت که نحوه تعریف آن به صورت زیر مدار را در نت لیست زیر مشاهده می کنیم.
پس می بینیم که زیر مدارات را می توان در چندین سطح تعریف کرد و محدودیتی از این لحاظ وجود ندارد و این به ساده تر شدن هر چه بیشتر کد نویسی ها و درک راحت تر آن منجر خواهد شد.
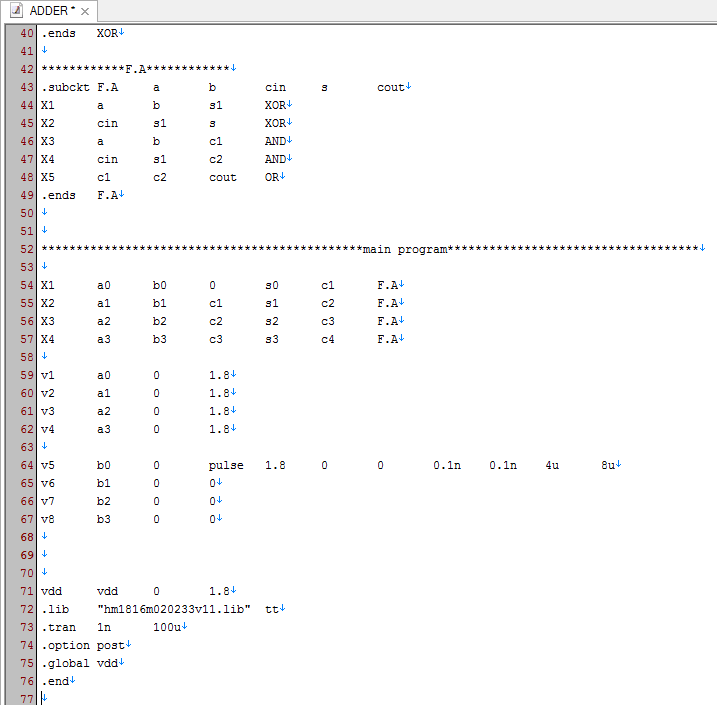
بعد از اینکه همه زیر مدارات را به طور کامل تعریف نمودیم اکنون آن را در برنامه اصلی (بعد از main program) فراخوانی خواهیم کرد. و در گام بعدی برای اینکه نشان دهیم جمع کننده رقم نقلی موجی طراحی شده به درستی کار می کند ولتاژهای ورودی را که در اصل بیت های باینری ورودی (a0-a3 , b0-b3) هستند به دلخواه تغییر می دهیم.
به طور مثال اگر بیت های a0-a3 را برابر ۱۱۰۰ باینری و بیت های b0-b3 را برابر ۱۰۰۰ قرار دهیم نتیجه جمع در خروجی که شامل بیت های c4,s3,s2,s1,s0 است باید به ترتیب برابر ۱۰۱۰۰ باشد.
نکته۷: در یک مدار cmos معمولاً یک منطقی را برابر ولتاژ VDD که در اینجا ۱٫۸ است در نظر می گیریم و صفر منطقی را هم برابر پایین ترین ولتاژ مدار که در این جا زمین است و مقدار آن صفر ولت می باشد در نظر خواهیم گرفت.
شبیه سازی یک جمع کننده رقم نقلی موجی ۴ بیتی در نرم افزار Hspice
همانطور که گفته شد برای شبیه سازی جمع کننده سربار نردبانی می توان حالت های مختلفی را برای ورودی ها در نظر گرفت و هر بار خروجی چک شود و با نتیجه مورد انتظار مقایسه صورت گیرد. اما امکان تست همه حالت های ممکن به خصوص اگر تعداد بیت ها بیشتر شود امکان پذیر نیست و در چنین مواردی تست را با استفاده از ADC , DAC ایده آل انجام می دهیم که چون بحث آن یک مقدار طولانی می شود آن را در یک آموزش جداگانه در آینده بررسی خواهیم نمود.
اما برای شروع کار همین روش را به ازای چنیدن ورودی مختلف تست می کنیم که از صحت عملکرد جمع کننده سربار نردبانی اطمینان کافی حاصل شود.
در این مثال خاص از جمع کننده رقم نقلی موجی همانطور که در نت لیست هم مشخص است ورودی های a0-a3 را برابر ۱۱۱۱ در نظر گرفته و b3-b1 را برابر صفر و ورودی b0 را به صورت پالسی تعریف می کنیم که بتوانیم تغییر بیت های خروجی را مشاهده کنیم و در شبیه سازی هم این مساله به وضوح دیده می شود.
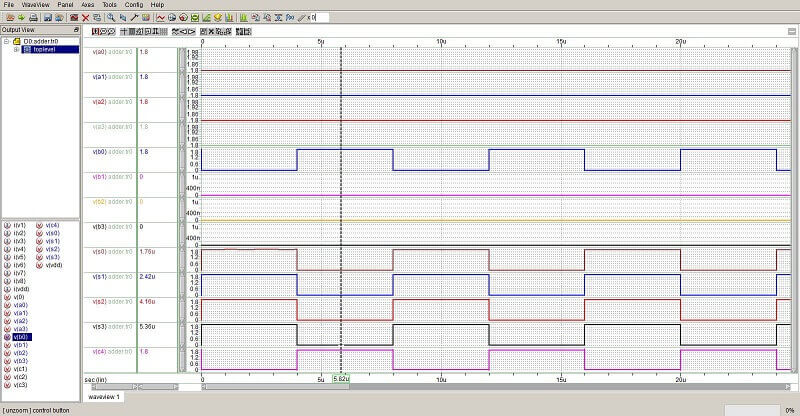
همانطور که انتظار می رود وقتی که b0=0 است بیت های خروجی c4,s3,s2,s1,s0 برابر ۰۱۱۱۱ هستند و به محض اینکه b0 از وضعیت صفر منطقی به یک منطقی تغییر کند بیت های خروجی هم به حالت ۱۰۰۰۰ تغییر خواهند کرد. در این شکل به وضوح می بینیم که یک بیت رقم نقلی در یک جمع کننده سربار نردبانی چه طور از کم ارزش ترین بیت خروجی یعنی s0 به صورت نردبانی به با ارزش ترین بیت خروجی یعنی c4 نقل مکان می کند.
نکته۸: اگر به بیت های خروجی که مقدار آنها صفر منطقی هستند دقت کنیم خواهیم دید که مقدار آنها دقیقاً برابر صفر مطلق نیست ولی در حد میکرو ولت است که در مقایسه با مقدار یک منطقی که حدود ۱٫۸ ولت می باشد بسیار ناچیز و قابل صرفه نظر است.
برای دریافت مشاوره انجام پروژه های دانشگاهی وارد صفحه انجام پروژه hspice سایت استاد راهنما شوید.



