در این آموزش از سری آموزشهای گام به گام نرم افزار Hspice در مورد مقایسه کننده دیجیتال که یک مدار ترکیبی است و بزرگتر ، کوچکتر و یا مساوی بودن دو عدد باینری را مشخص می کند صحبت خواهیم نمود. ابتدا مقدمه ای درباره مقایسه کننده ها و انواع آنها خواهیم داشت.
در بخش بعدی در مورد مقایسه کننده اندازه بدون علامت (Unsigned magnitude comparator) صحبت کرده و مکانیسم کار آن را شرح داده و خواهیم دید که هسته اصلی این نوع از مقایسه کننده ها در اصل یک جمع کننده می باشد که در آموزش چهارم در مورد انواع جمع کننده ها صحبت کردیم و در انتهای مقاله شماتیک مداری یک مقایسه کننده ۸ بیتی را وارد محیط کدنویسی Hspice کرده و به ازای حالت های مختلف ورودی ها ، مقایسه کننده دیجیتال را شبیه سازی خواهیم کرد.
مقدمه ای در مورد مقایسه کننده های دیجیتال
هدف از ساخت یک مقایسه کننده دیجیتال تشخیص برابری یا نابرابری (بزرگتر یا کوچکتر) بودن دو عدد باینری است که بسته به نوع آن یک مقایسه کننده می تواند تساوی دو عدد یا مقایسه تمامی حالات ممکن را نسبت به هم در برگیرد و اگر یکی از این حالت ها (تساوی ، بزرگتر یا کوچکتر بودن دو عدد) رخ داد یک سیگنال on (یک منطقی) در خروجی متناظر با آن حالت خواهیم داشت .که از این سیگنال می توانیم در جاهای مختلف مدارمان و برای اهداف متفاوت استفاده کنیم.
برای اینکه بهتر بتوانیم کاربرد یک مقایسه کننده دیجیتال را درک کنیم با یک مثال عملی شروع خواهیم کرد.
فرض کنید سطح مایع داخل یک تانکر را توسط سنسور تشخیص سطح به یک کمیت الکتریکی (مثلاً ولتاژ) تبدیل کرده ایم و برای ذخیره سازی و پردازش بهتر اطلاعات سیگنال ، آن را توسط یک مبدل آنالوگ به دیجیتال (ADC) از حالت آنالوگی به دیجیتالی تبدیل نموده ایم حال دیتای سیگنال دیجیتالی را که در واقع نشان دهنده سطح مایع است با عدد باینری که مد نظر ماست (فرض کنید این عدد نشان دهنده پر شدن تانکر باشد) توسط مقایسه کننده دیجیتال مقایسه خواهیم کرد.
اگر سطح مایع از سطح مجازی که تعریف کرده ایم بالاتر رود مقایسه کننده دیجیتال یک تغییر وضعیت در خروجی تساوی خواهیم داشت (سطح ولتاژ خروجی از صفر به یک یا بلعکس تغییر می کند) که دقیقاً مانند CLK عمل می کند که لبه بالارونده یا پایین رونده این CLK می تواند فرمان قطع یا وصل شیرهای داخل تانکر را صادر کند و سطح مایع کنترل شود.
مثال فوق یک مثال ساده از کاربرد مقایسه کننده دیجیتال بود و در واقع کاربرد مقایسه کننده در مدارات دیجیتال بسیار گسترده تر است. مقایسه کننده ها انواع مختلفی دارند از جمله مقایسه کننده اندازه که در ادامه به آن خواهیم پرداخت ، مقایسه کننده برابری که فقط تساوی دو عدد را نشان می دهد ، مقایسه کننده k=A+B که اگر جمع دو عدد A , B برابر k شود خروجی آن برابر یک خواهد شد و …
دسته بندی دیگری که برای مقایسه کننده ها می توانیم داشته باشیم بر اساس علامت دار یا بدون علامت بودن مقایسه کننده است که ما اینجا فقط مقایسه کننده های بدون علامت را بررسی می کنیم و برای کسب اطلاعات بیشتر در مورد مقایسه کننده دیجیتال می توانید به مقالات سایت IEEE و یا کتابهای رفرنس موجود مانند کتاب weste مراجعه کنید.
مقایسه کننده اندازه بدون علامت
یک مقایسه کننده دیجیتال اندازه (Digital Magnitude Comaprator) برای تشخیص بزرگتر یا کوچکتر و حتی مساوی بودن دو عدد باینری به کار می رود که در شکل زیر شماتیک آن را مشاهده می کنیم. هسته اصلی مقایسه کننده اندازه از یک تفریق کننده تشکیل شده است که خود تفریق کننده نیز در اصل یک جمع کننده است که ورودی اول (مفروق منه) را با متمم به علاوه یک ورودی دوم (مفروق) جمع خواهد کرد بدین ترتیب تفریق دو عدد از هم حاصل خواهد شد. A-B=A+B’+۱ .
که متمم به علاوه یک عدد دوم یعنی مفروق را از طریق معکوس کردن بیت های آن و جمع کردن با یک بدست خواهیم آورد که برای جمع عدد باینری دوم با یک رقم نقلی ورودی تمام جمع کننده اول را این بار به جای زمین به VDD متصل خواهیم کرد با این روش خواهیم توانست یک تفریق کننده بدون علامت داشته باشیم که دو ورودی باینری را از هم تفریق می کند.
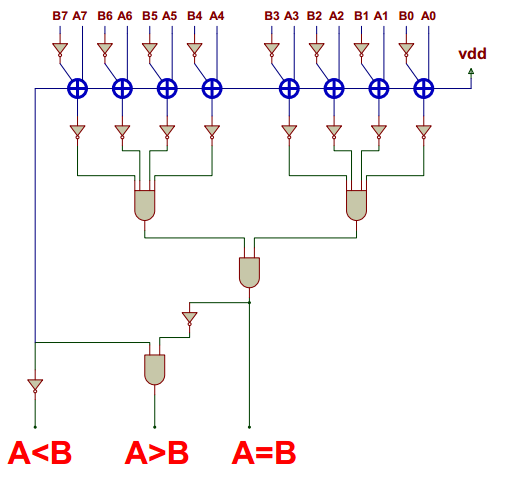
حال اگر یک سرریز اتفاق بیفتد به این معنی است که عدد باینری اول (مفروق منه) بزرگتر یا مساوی عدد باینری دوم (مفروق) است B ≥ A . پس برای تشخیص بزرگتر یا مساوی بودن عدد اول از عدد دوم کافیست رقم نقلی آخرین بیت تفریق کننده چک شود.
برای تشخیص تساوی دو عدد نیز می توان از یک آشکار ساز صفر که در اصل از گیت های not و AND تشکیل شده است استفاده نمود بدین صورت که اگر دو عدد مساوی هم باشند بیت های خروجی تفریق کننده تماماً صفر خواهد شد پس اگر همگی را معکوس کرده و با هم AND کنیم یک بودن خروجی گیت های AND به این معنی است که دو عدد باینری با هم برابر هستند A=B .
گفتیم که رقم نقلی خروجی بیت آخر A ≥ B را نتیجه خواهد داد پس اگر رقم نقلی را معکوس کنیم A < B را خواهیم داشت. و برای تشخیص A > B از یک گیت AND که خروجی رقم نقلی بیت آخر را با متمم تساوی بیت ها AND می کند استفاده خواهیم کرد. پس دیدیم که یک مقایسه کننده دیجیتال به سادگی با استفاده از مدارات منطقی قابل پیاده سازی است.
سوالی که ممکن است پیش بیاید این است که برای پیاده سازی مدار تفریق کننده چه نوع جمع کننده ای باید استفاده کنیم؟ در پاسخ باید بگوییم که همه چیز بستگی به شرایط دارد.
به طور مثال اگر اولویت طراحی ها فقط پایین بودن توان مصرفی باشد و سرعت دارای اهمیت نباشد همان جمع کننده سر بار نردبانی را که در جلسه چهارم در مورد آن صحبت نمودیم را به کار خواهیم گرفت اما اگر سرعت در درجه اول اهمیت قرار داشته باشد و تعداد بیت های مقایسه کننده هم بیشتر شود تاخیر افزایش خواهد یافت و جمع کننده رقم نقلی موجی پاسخگوی نیاز ما نخواهد شد و باید از جمع کننده های سریعتر همچون tree adder یا CLA استفاده کنیم.
کد نویسی و شبیه سازی مدار مقایسه ۸ بیتی در نرم افزار Hspice
طبقی روالی که گفتیم اینجا نیز اول زیر مدارات مقایسه کننده دیجیتال را تعریف می کنیم که شامل گیت های منطقی و تمام جمع کننده است و در جلسات گذشته همگی آنها را (به غیر از گیت AND چهار ورودی که نحوه کد نویسی آن مانند حالت دو ورودی بوده و نیاز به توضیح خاصی ندارد) بررسی کردیم. پس مستقیماً سر برنامه اصلی که شامل فراخوانی زیر مدارات نوشته شده است می رویم.
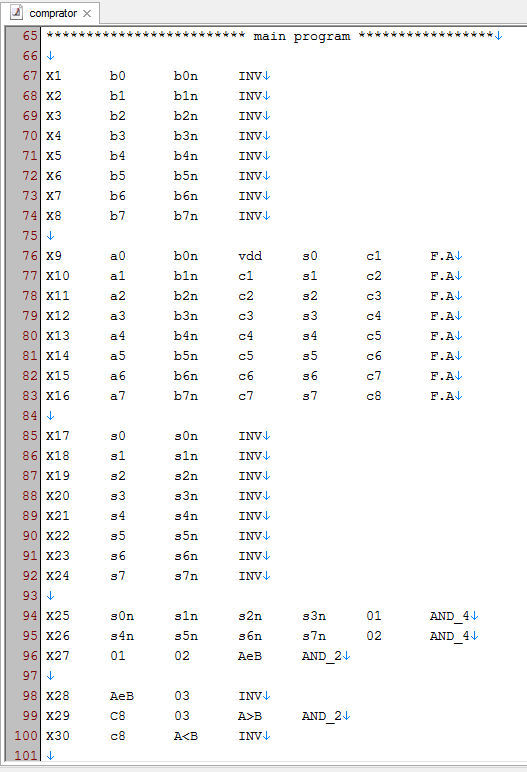
می بینیم که نحوه کد نویسی برنامه اصلی مقایسه کننده دیجیتال هم بسیار ساده بوده و با انتخاب درست اسم گره های مدار به سادگی می توانیم نت لیست مان را بنویسیم.
در برنامه اصلی ابتدا گیت های not ورودی را که متمم ساز ورودی باینری B هستند را تعریف می کنیم (X1-X8) بعد تمام جمع کننده ها را فراخوانی خواهیم کرد (X9-X16) پس از تعریف تفریق کننده حال مدار تشخیص تساوی دو ورودی شامل گیت های not و گیت های AND را مشخص کرده (X17-X27) و در انتها مدارات تشخیص بزرگی را ( B>A , A>B) که شامل گیت AND و گیت های not انتهایی مقایسه کننده دیجیتال است فراخوانی خواهیم نمود (X28-X30).
اسم گره های مدار گویای همه چیز است و ترتیب نوشتن زیر مدارات هم به گونه ای است که از بالا به پایین و به ترتیب همه المان های مدار مقایسه کننده دیجیتال تعریف شده اند. اگر با این استاندارد کد نویسی کنیم درک آن توسط دیگران و حتی خودمان بسیار ساده تر خواهد شد و نحوه عیب یابی مدار نیز به سادگی ممکن خواهد بود. و خیلی وقت ها برای شبیه سازی مدارات نیاز خواهد شد که بخش کوچکی از مدار را تغییر دهیم که اگر کد نویسی ها درهم بر هم باشد واقعاً کار سخت خواهد شد.
بعد از نوشتن برنامه اصلی مقایسه کننده دیجیتال در نرم افزار Hspice برای تست عملکرد مدار باید ورودی های متناسب را به مقایسه کننده اعمال کنیم. نحوه تست مدار بدین صورت می باشد که ورودی های کم ارزش تر a0 ، b0 را به صورت پالسی تعریف کنیم (دوره تناوب b0 را دو برابر a0 در نظر می گیریم ) و بقیه ورودی ها را مقداری ثابت و برابر هم انتخاب خواهیم کرد.
نتیجه شبیه سازی به ازای ورودی های گفته شده به شکل زیر در خواهد آمد.
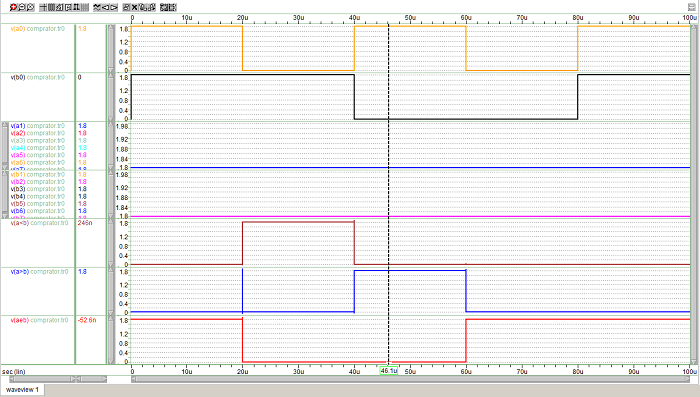
همانطور که از نتیجه شبیه سازی پیداست در ابتدای کار تا ۲۰us دو ورودی باینری A , B کاملاً برابر هستند پس پس خروجی تساوی aeb بالا خواهد بود از ۲۰us به بعد تا ۴۰us ورودی B بزرگتر از ورودی A خواهد شد پس خروجی a
نکته: در زمان ۲۰us که ورودی a0 از یک به صفر تغییر وضعیت می دهد و حالت پایین روندگی دارد خروجی a>b بر خلاف انتظار برای مدت زمانی کوتاه به سمت بالا صعود کرده و دوباره به سر جای خود بازخواهد گشت که این پدیده را گلیچ می گویند و چون بحث کردن در مورد آن مقداری زمان بر است در یک جلسه جداگانه در مورد علت پیدایش گلیچ ها و مشکلاتی که در عملکرد مدار ایجاد خواهند کرد و نحوه رفع آنها صحبت خواهیم کرد.
برای دریافت مشاوره انجام پروژه های دانشگاهی وارد صفحه انجام پروژه hspice سایت استاد راهنما شوید.



